Man don't get angry implementation suggestions

Introduction

Recently, I got a simple yet intriguing project: to create a “Man Don’t Get Angry” game. An idea struck me immediately on how to approach it. This assignment, intended for a group of students, opened up many creative possibilities. In this blog, I’m excited to share my concept with you.

Rules

1. Objective: The main goal is to move all four of your game pieces around the board and into your “home” row before your opponents.
2. Players: The game is typically played by 2 to 4 players.
3. Starting the Game: Each player chooses a color and places their four pieces in the corresponding starting area. Players take turns rolling a die, and the one who rolls the highest number starts the game. To move a piece out of the starting area onto the track, a player must roll a six.
4. Movement: Players take turns rolling a single die and move one of their pieces clockwise around the board according to the number rolled. Rolling a six grants another turn. If a piece lands on a space already occupied by an opponent’s piece, the opponent’s piece is sent back to their starting area.
5. Safe Spaces: Certain spaces on the board are marked and are safe from capture. Pieces on these spaces cannot be replaced by opponents’ pieces.
6. Home Stretch: Once a piece has completed a full circuit of the board, it enters the “home” row or column. This is a colored path leading to the “home” spaces.
7. Winning the Game: The first player to get all four of their pieces into their “home” spaces wins. The game can continue to determine the second, third, and fourth places.

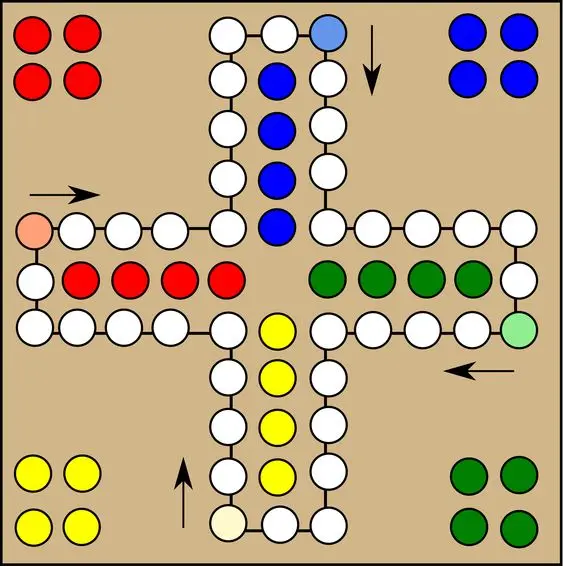
Board

“Man Don’t Get Angry” is a classic board game similar to “Ludo.” The game board typically features a square layout with a cross-shaped, color-coded track in the center, divided into four arms. Each arm has three rows of squares, with the middle row used as the player’s home column. At the end of this column, there’s a larger square or circle, often labeled as the “home” or “finish” area.

Each of the four corners of the board contains a player’s starting area, distinguished by distinct colors (usually red, green, yellow, and blue). These areas often have four slots or circles where the player’s pieces begin the game.

The game’s objective is for players to move their pieces around the board and into their home column by rolling a die. The challenge comes from pieces being sent back to their starting area if another player lands on the same square.

The design is simple yet colorful, emphasizing clear demarcation of each player’s path and home area. The central part of the board, where the arms of the cross intersect, is often embellished with decorative elements related to the game’s theme.

Implementation

I want to start by discussing what the board looks like and how we would represent it in data structures.

Naive approach

You can see that the board looks like a plus sign. Intuitively, you may want to represent it as a matrix and fill this matrix with some objects (such as the players’ row and the finish area). Then put the players in the correct positions and move them along the row in the correct direction.

This approach is OK, but it has a number of problems:

1. Too many invalid states. When you move your player, he can be moved in the wrong direction 75% of the time (you have up, down, left, right directions, but only one is correct).
2. It is too difficult to calculate the next position. We can’t quickly decide which way to move the player. The easiest way is to remember each player’s previous position and move in the opposite direction. But this is where we face the problem of the twists and turns.

Better approach

I propose a simpler solution.

Previously, I described the path that a player moves along as a ‘row’. This path is homeomorphic to a circle. The player can only move forward, with no option to move backwards.

Suppose our board is of size $x \times x$ (where $x$ is an odd, positive number). Then, the length of the path is $4 * (x-1)$.

The starting position for the first player is $0 * (x-1) = 0$, positions for the second, third, and fourth players are $1 * (x-1)$, $2 * (x-1)$, and $3 * (x-1)$ respectively.

We can easily calculate a player’s next position as follows:
$player.position = player.position + steps$

When a player collides with another, set another’s player position to the spawn:
$player.position = player.color * (board.size - 1)$

If a player’s position exceeds his spawn point $-1$ it is in the finish area (or home area). So representation of home can be various. For example, we can set player’s position to the negative number (the specific implementation is not important in this example, the main thing is that the players do not collide)

When a player is in the finish area, they can only move forward.

The finish area’s length is $\frac{x-1}{2} - 1$.

Conclusion

Anyway, which variant you choose is up to you. I think I’ve explained simply enough how I see modeling this game.